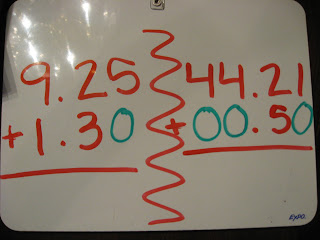Fraction to decimal conversion

Fraction to decimal conversion can be very confusing. I learned to do this in class this week and it really is not as bad as you may think. This conversion all has to do with where you need to move the decimal to make the problem right. You need to ask yourself: "do I move it to the left or right?" There are many types of fractions you might encounter to convert into decimals. These might include proper fractions, mixed fractions, and improper fractions. http://www.learningwave.com/chapters/decimal13/basics/convert.html You may look at the few examples I provided and look at what I did. Look above. Use this website above to help you.

Fractions and decimals represent the same things. They are numbers that are not whole. Please use this website to help you better understand how to convert fractions to decimals. whole.http://webmath.com/fract2dec.html

Fraction to percentage conversion

Changing fractions to percents is not hard. There are a few simple steps to follow when doing this. First, divide the numberator by the denominator. Next,  you need to multiply the fraction by 100. Last, you need to round the answer to the nearest whole number. You may look at the examples I provided. You may also use this website to help you better understand how to convert fractions to percents. http://www.mathgoodies.com/lessons/vol4/fractions_to_percents.html

Let's say we have the problem 1/5. What do we do first? We need to do 1/5, which is .2, now multiply by 100. You should come up with the number 20. Which is also 20%. Great job! Let's do another one. How about 1/8. This comes to .125, now multiply this by 100. You should come up with 12.5%. Did you?

Integers or signed numbers

When doing integers or signed numbers there are a few important things to remember. When dividing two negative integers, the answer will always be a positive number. When multiplying two negative integers, the answer will always be a positive number as well. Let's look at a few examples: -2(-7)=14, and -56/-7=8. Now, when you have a positive and negative number problem such as 4(-5), the answer will always be a negative. So, the answer is -20.

What if you have 0/(-2), since we are dividing by zero, the answer is 0. Let's switch that problem around, now we have -2/0. Can we do this? No, the answer is undefined. When we subtract integers such as -1-5, we move to the left of the number line. This answer is -6. Now, we have the problem 5-(-3). What do we do? Two subtraction signs next to each other means to add them together. The answer is 8. You may look at the examples I provided above. http://www.mathleague.com/help/integers/integers.htm You may use this website to better help you understand how to do integer problems.

Multiplying is easy!

I learned in class this week that there are three simple steps in multiplying fractions. The three simple steps are to first muliply the top numbers which are the numerators, then multiply the bottom numbers which are the denominators, last simplify the fraction if needed. You can look at my examples above. The easy thing about multiplying fractions is you do not have to worry about getting the denominators to be the same number. The link that you see here http://www.youtube.com/watch?v=19s-HKWQmMw will help you better understand fraction multiplication.
When you simplify fractions, you need to ask yourself what can I divide by using both numerator and denominator to get "nice" numbers. Let's say you would like to simplify this: 16/24. First you need to ask yourself what is the number I can divide both numbers by? That number is 4! So now you have, 4/6. Can you simplify this? Yes you can! Let's divide by 2. So now you have 2/3.  Great job! There is much more to multiplying fractions, I gave you the basic steps.

Fraction Addition

There are three simple steps to adding fractions. First, you need to make sure the bottom numbers (the denominators) are the same. Next, add the top numbers (the numerators) and put the answer over the same denominator. Last, simplify the fraction if needed. Let's say we have the problem: 5/8 + 2/8. The top numbers (the numerators) are not the same, but the denominators are the same. So, we just add the top numbers together to get 7/8. Here are some additional examples:

Let's say we have the problem 4/5 + 3/5. What do we do? Well, start off with adding the numerators together to get 7, then put it all together. So, now we have 7/5. Great job! Use this link to help you with adding fractions. It's is a great game to do with your students. http://funschool.kaboose.com/fun-blaster/back-to-school/games/game_action_fraction.html

Decimal Addition

To add decimals, you must write one above the other with their decimal points lined up, like this: look above.
What I learned this week, is simple steps to remember when adding decimals. First, you need to write down the numbers, one under the other, with the decimal points lined up. Next, put in zeros so the numbers have the same lenth. Last, add normally, remembering to put the decimal point in the answer.

Where one decimal doesn't have digits that the other one does, you put in zeroes, like this: look above.

Now, it's easy! You just add the two numbers as you would two whole numbers, with carries if necessary, but you keep track of where the decimal point goes and put it in the result right under the decimal points in the two numbers being added, like this: look above. Use this link to help you with adding decimals.  http://www.onlinemathlearning.com/adding-decimals.html